Clustering
Josh Moller-Mara
What's clustering?
- Clustering, in its broadest form, is figure out how to group data
- It's generally a form of unsupervised learning. Which is to say that you don't know a priori which data belong to which groups.
- It's often used in
- Text mining to find topics
- Image recognition, image segmentation, brain region segmentation
- Spike sorting
- Bioinformatics, gene families
- Marketing: Shopping habits, trends, recommendations
- Anomaly detection
Types of clustering
- Combinatorial algorithms - work directly on the observed data with no direct reference to an underlying probability model
- Mixture modeling - supposes that the data is an i.i.d sample from some population described by a probability density function
- Mode seekers - "bump hunters" take a nonparametric perspective, attempting to directly estimate distinct modes of the probability density function
Combinatorial clustering
$k$-means
Agglomerative clustering
$k$-means
- Assign points to a cluster
- For each cluster, calculate it's mean center point
- Assign points to a cluster based on the closest center
- Repeat steps 2-3 until no point changes cluster
$k$-means
Problems with k-means
- Dependent on initial conditions
- Only linear boundaries
- Clusters tend to be around the same size
- What if cluster is inside another?
- How do you know how many clusters to use?
- Outliers? Use $k$-medoids
Agglomerative single-linkage
Agglomerative single-linkage clustering is one of several "bottom-up" types of hierarchical clustering.- Start with each point in its own cluster
- Compute the distances of each cluster
- In this case, find the two closest points between clusters
- In other cases you take the average distance of points between clusters
- In complete-linkage you find the furthest points between clusters
- Merge the two clusters with the minimal distance
- Repeat steps 2 and 3 until you have the desired number of clusters
Agglomerative single-linkage
Single-linkage clustering
- Naive implementation is $O(n^3)$ slow
- Exhibits "chaining". Points in the same cluster can be further away from each other than from a point in another cluster.
- Again, how do you know how many clusters to use?
- Alternatives?
- Complete-linkage clustering
- Average-linkage clustering
- Also, spectral clustering
Agglomerative
The importance of representational space
RGB Space

HSV Space

LAB Space

Mixture Modeling
How would you fit this?
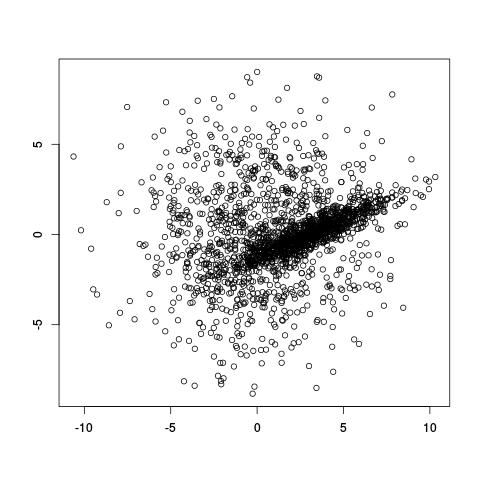
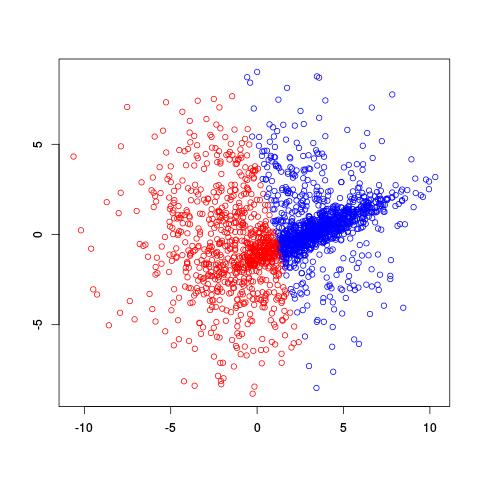
$k$-means doesn't do too well
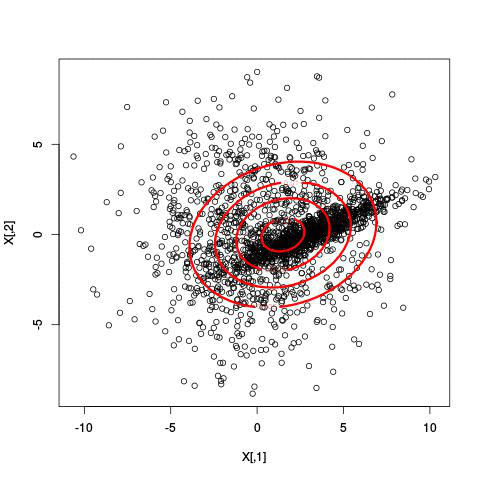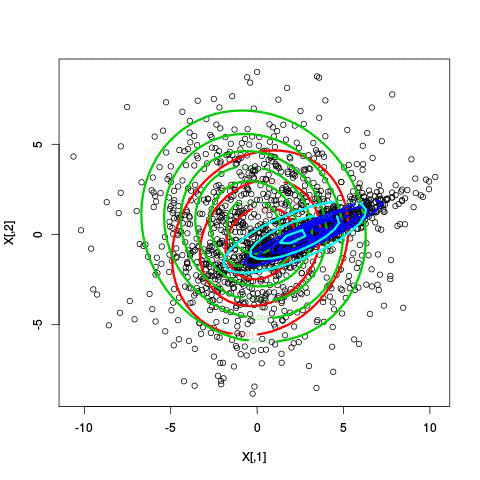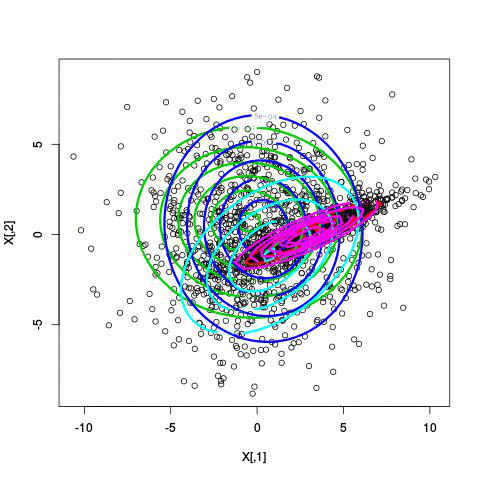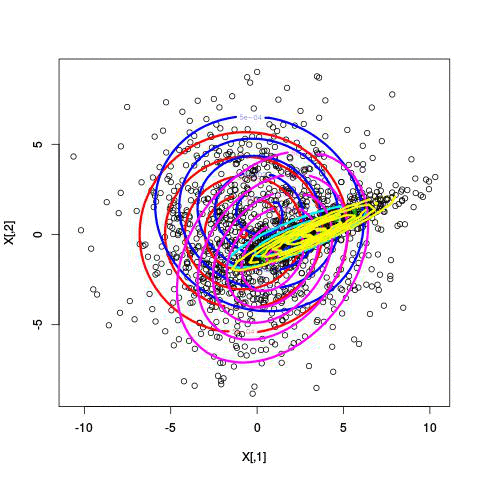
Use Gaussian mixture modeling!
\[p(x) = \sum_{i=1}^k \alpha_i \cdot \text{N}(x|\mu_i, \sigma^2_i)\]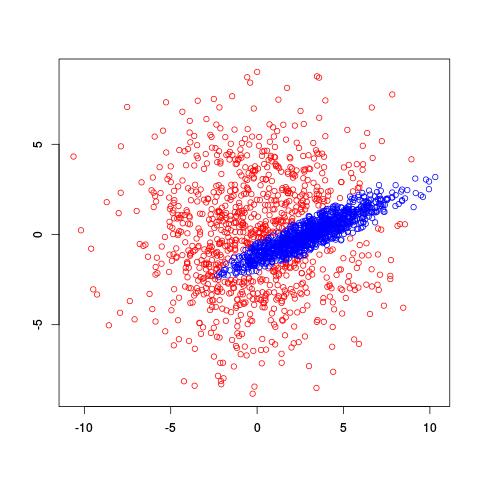
Expectation-Maximization algorithm
- Gaussian mixture models are fit similarly to $k$-means
- But you assign points a probability for each mixture, instead of outright assigning. This is called the expectation step
- In the maximization step, you take all the points and their cluster-probabilities and find the best-fitting Gaussian for each cluster. You estimate both the mean and the covariance
Example EM-iteration
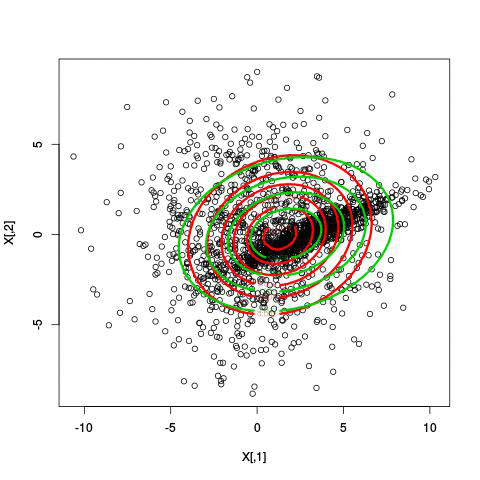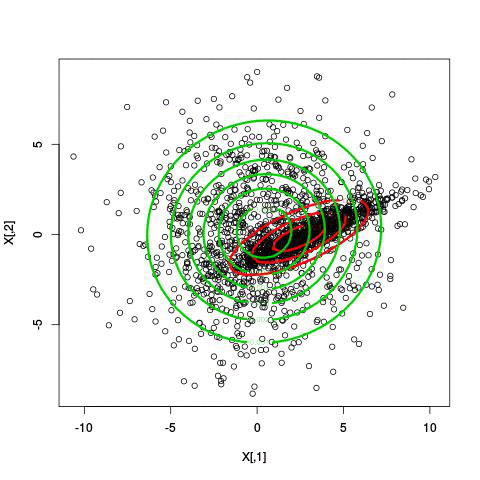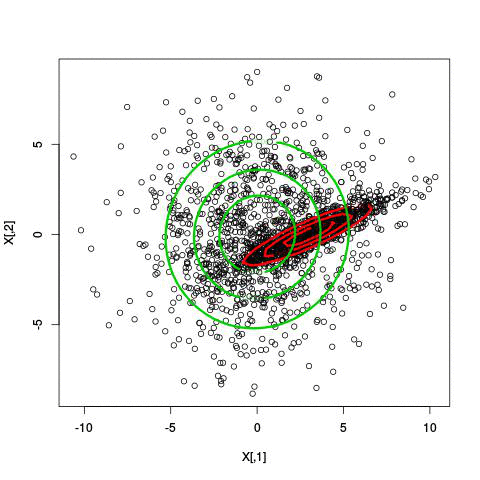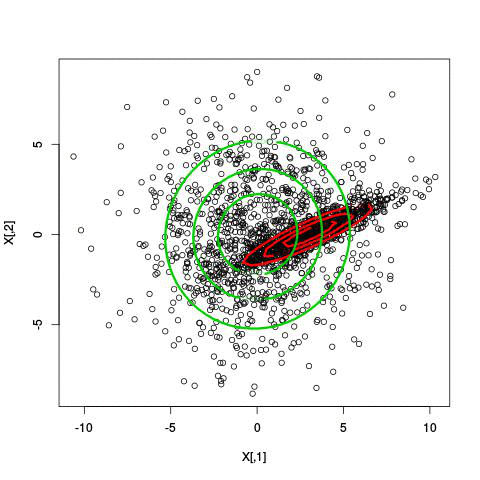
Comments on the EM algorithm
- Like $k$-means, it's sensitive to initial conditions
- However, you get not just an assignment but the probability a point is in each cluster
- You can use the likelihood with a model scoring mechanism like AIC or BIC to count the number of clusters
- Mixture models, however, can also be fit using Markov-Chain Monte Carlo methods like Gibbs sampling
Fitting different numbers of clusters
Latent Dirichlet Allocation for topic modeling
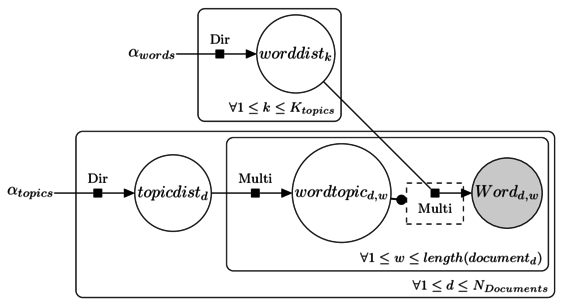
LDA topic modeling in JAGS
model {
for (k in 1 : Ktopics ) {
worddist[k,1:Nwords] ~ ddirch(alphaWords)
}
for( d in 1 : Ndocs ) {
topicdist[d,1:Ktopics] ~ ddirch(alphaTopics)
for (w in 1 : length[d]) {
wordtopic[d,w] ~ dcat(topicdist[d,1:Ktopics])
word[d,w] ~ dcat(worddist[wordtopic[d,w],1:Nwords])
}
}
}
LDA topic modeling in JAGS (cont)
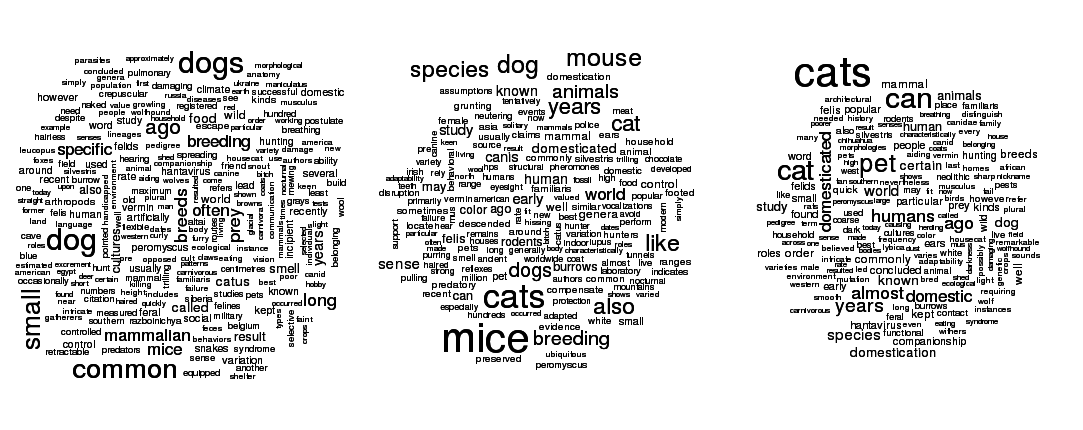 An example of LDA run on Wikipedia articles on cats, dogs, and mice.
An example of LDA run on Wikipedia articles on cats, dogs, and mice.
Wrapping Up
- Which clustering algorithm you use depends on your assumptions
- Central to clustering is the idea of distance. What space you use or how you define distance have a great impact on what clusters you get.